Part One here.
I told Warren that I would write once more about Fermat's Enigma, Singh's brilliant story of Allan Wiles twenty year quest to solve the last theorem, the mathematical riddle that had stumped the world for the last 350 or so years. I finished the book and have to admit that I cried a little bit at the end. Never have got emotional about math before but the human aspect of the book was actually quite moving.
As I have stated before, unlike my brilliant siblings, I am no math genius. I was dragged kicking and screaming through quadratic polynomials. I swear that my algebraic defeat still burns and I am tempted to have another go at it and see if I can crack the lexicon before I finally expire.
I loaned the book out and don't have anything to consult but will try to regale you from memory with a couple tidbits in order to convince you to get it yourself and give it a read. First the concept of amicable numbers.
*
Did you know that the numbers 220 and 284 are called amicable numbers? Their mathematical significance was known to the ancients as far back as biblical times and perhaps earlier. Amicable numbers are pairs in which the sum of the proper divisors of each is equal to the other number.
The divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110, the sum of which add up to 284. The divisors of 284 are 1, 2, 4, 71 and 142, of which the sum is 220. This is the smallest pair, other pairs include (1184, 1210), (2620, 2924), (5020, 5564) and (6232, 6368).
The Pythagoreans thought that these pairs were imbued with mystical power. Their general formula was developed in 850 by the great Iraqi mathematician Thābit ibn Qurra (826–901.) Fermat, Euler and Descartes all played with Qurra's formula.
This is Qurra's formula: if
p = 3 × 2n − 1 − 1,
q = 3 × 2n − 1,
r = 9 × 22n − 1 − 1,
where n > 1 is an integer and p, q, and r are prime numbers, then 2n×p×q and 2n×r are a pair of amicable numbers.
 |
| Rubens - reconciliation of Jacob and Esau |
Talismans and charms with one or the other number inscribed were sometimes used in the middle ages to attract lovers, at times a suitor would swallow something printed with one number and slip the other number into the drink of the object of his or her intentions. Or wear them as amulets with similar goals.
Here is a rather cabalistic look at the first two amicable numbers. Please do not ask me for an explanation. I was as bad at the sephiroth as I was at math.
*
 |
| 1927 play that introduced the truel |
Imagine a duel but with three protagonists instead of two. Let's say they are badass gunfighters. The first desperado we shall call Mr. Apple, the second Mr. Banana, and the third Mr. Cherry. These varmints have done pissed each other off and decide to fight a truel.
Each gets a gun and they take turns shooting at each other until, as usually happens in such matters, only one person is left. Mr. Apple, who hits his shot 1/3 of the time, gets to shoot first. Mr. Banana, who hits his shot 2/3 of the time, gets to shoot next, assuming he is still alive. Mr. Cherry, who hits his shot all the time, shoots next, assuming he is also alive. The cycle repeats. If you are Mr. Apple, the worst shooter, who should you shoot first for the highest chance of survival?
This one takes some pondering. In fact it a bit counterintuitive. In a probability sense Mr. Apple, the worst shot, has a 52% chance of winning if he does the smart thing.
Which is to fire his gun into the air.
In this way, the second desperado and second best shot, Mr. Banana, will most likely shoot at Mr. Cherry, who has the greatest likelihood of killing him. Mr. Banana has a 18% chance of survival while the best shot, Mr. Cherry, has a 30% chance of living. But Apple gets the next shot in the rules of the game. And has significantly increased his chances of survival.
 |
| Hey tough guy, my innate effeminate tendency towards beta subordination is ultimately going to clean your well toned clock! |
A link to the math behind the answer.
*
I digress regarding the Fermat book. Hard to put down. The greatest benefit was the introduction to some of the amazing mathematicians of ancient and modern times, Euler, Fermat, Shimura and Tamiyama, Germane, Turing, the book gives us great vignettes of some truly brilliant people. Makes me wish I had paid more attention in class.
*
The book makes the interesting observation that just because something works for the first million or so numbers doesn't necessarily hold for million + 1. And half of infinity is still infinity. As is twice infinity.
*
A photon checks into a swank hotel. The man at the front desk asks him if he has any luggage. The photon looks at him and says, "You know, I'm really traveling light."




.jpg)
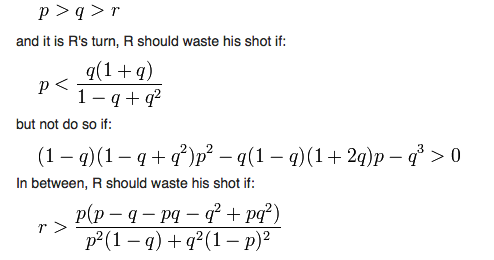
No comments:
Post a Comment